Gradient Descent Algorithm and Batch

2017-09-23

梯度下降法（Gradient Descent Algorithms），我们似乎都知道。同时，在深度学习中，大家对于Batch这个词并不陌生。我第一次听到是在一个技术分享会上面，嘉宾说“大家对Batch size的选择嘛，一般都是64之类的”，不明觉厉。今天，就来总结一下，当我们在谈论Batch的时候，我们究竟再说点什么。

1. 梯度下降法

在深度学习里面，梯度下降法是一种比较常见的优化求解算法。根据在优化更新参数时，每次选取的样本的数量，我们将梯度下降法，具体地分为以下三类。

批量梯度下降法（Batch Gradient Descent）

小批量梯度下降法（Mini-batch Gradient Descent）

随机梯度下降法（Stochastic Gradient Descent）

2. 批量梯度下降法

批量梯度下降法（Batch Gradient Descent），第一眼不明觉厉，看着并不知道这个方法是什么。其实，批量梯度下降法，就是最最普通的梯度下降法，也即在优化更新参数的时候，我们每次选取的样本数量为所有的样本。
具体地，假设$ X = [X^{(1)}, X^{(2)}, …, X^{(m)}]$, $Y = [Y^{(1)}, Y^{(2)}, …, Y^{(m)}]$，其中，$ X^{(i)}$ 为第 $i$ 个训练样本的维度为$n_{x}$预测变量，$ Y^{(i)}$ 为第 $i$ 个训练样本的响应变量，$ m $ 为样本总数。
每轮参数迭代的时候，批量梯度下降法把所有的训练样本 $(X, Y)$ 都考虑进去一起计算。
缺点，每个迭代训练的时间较长，效率较低。

3. 随机梯度下降法

随机梯度下降法（Stochastic Gradient Descent），指每次参与参数迭代的样本量只有一个。
缺点，每次训练的时候，只采用一个训练样本，一个训练样本会带来过多的随机性，不能保证训练时候的损失函数可以收敛，即便收敛，也需要耗费比其他方法更久的迭代次数；同时，就没有了每个iteration训练时，向量化的操作的便捷性。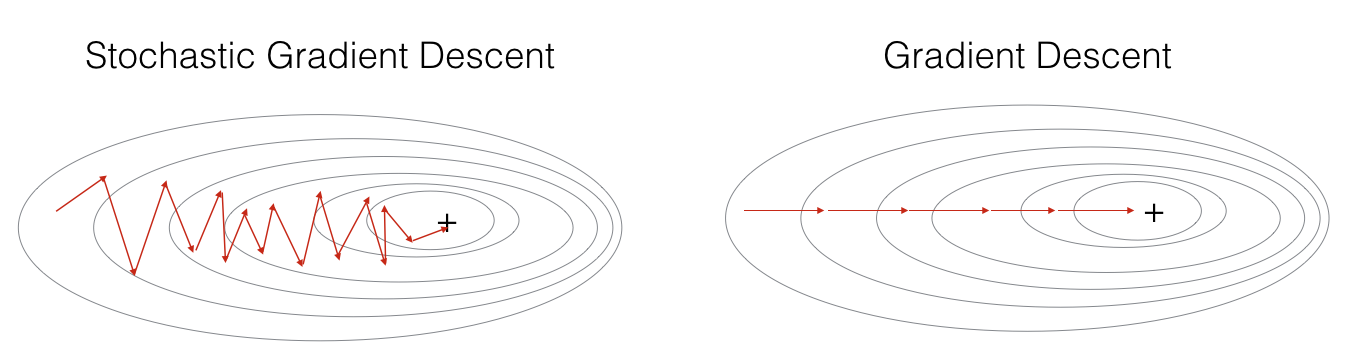

4. 小批量梯度下降法

小批量梯度下降法（Mini-batch Gradient Descent）的每轮迭代的样本量较小，因而，称冠上小批量（mini-batch）的名称。具体地，将所有的训练样本分成等量的小样本（当然，最后剩下的那份并不苛求和其他小样本的样本容量相等），每轮参数迭代的时候，都在各个小样本上面训练。其中，等量的小样本的样本容量称为批量大小（Batch size），这是一个对于模型而言的超参数（hyper parameter），可以去调整（tune）。通常用的batch size是 $64$ 。
具体地，假设$ X = [X^{(1)}, X^{(2)}, …, X^{(m)}]$, $Y = [Y^{(1)}, Y^{(2)}, …, Y^{(m)}]$，其中，$ X^{(i)}$ 为第 $i$ 个训练样本的维度为$n_{x}$预测变量，$ Y^{(i)}$ 为第 $i$ 个训练样本的响应变量，$ m $ 为样本总数。设Batch size为 $m_1$，即可以记每一个小样本$ X^{\lbrace k \rbrace} = [X^{(k)}, X^{(k+1)}, …, X^{(k-1+m_1)}]$，即到时迭代参数的时候，就在每个 $ X^{\lbrace k \rbrace}$ 上面去迭代。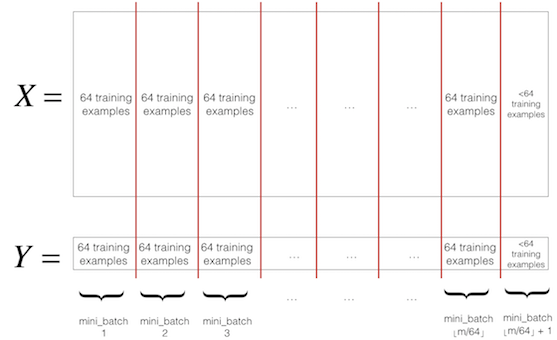

小批量梯度下降法的应用场景为当样本量较大时，可以考虑使用小批量梯度下降法，具体的batch size可以选择$2^k, k = 6, 7, 8, 9, 10.$ 即$64, 128, 256, 512, 1024$；
当样本量 $m<2000$ 时，使用批量梯度下降法（Batch Gradient Descent）。

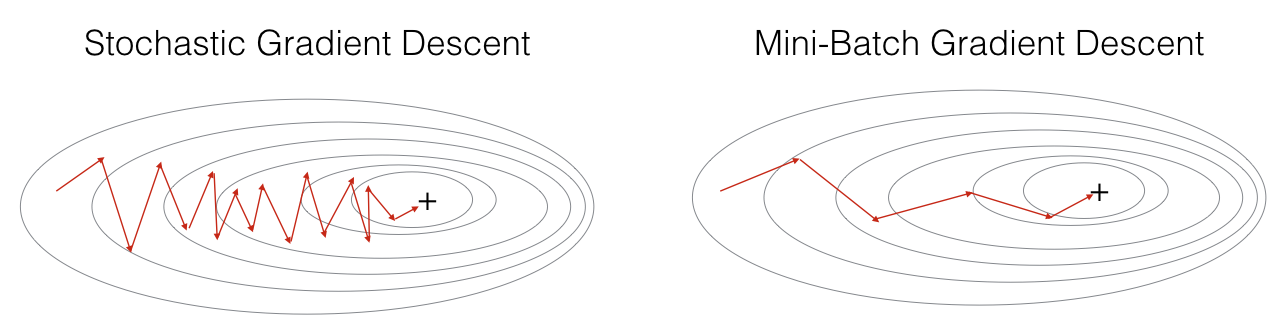
需要注意：

做小批量梯度下降法的时候，首先需要将样本打散，防止样本内部的某些结构性干扰后续参数迭代训练。
全局只用到一次参数的初始化。即，最开始的时候需要做一次参数初始化，然后，开始在$ X^{\lbrace 1 \rbrace} $上面做训练，经过迭代以后，得到参数，假设是 $w_1, b_1$ ，然后，将 $w_1, b_1$ 的值带入到$ X^{\lbrace 2 \rbrace} $ 的训练中去，经过迭代得到 $w_2, b_2$ ，以此往后。