Probability Calibration

2017-08-31

1. 背景介绍

在许多情况下，我们可以得到这样一个分类器，它能够预测某测试样本的分类标签，然而，却无法一致地给出相对应的该测试样本属于类别c的概率估计$P(c|x)$。有些时候，该分类器会提供一个得分，暂且记为$S(x)$，其中$S(x)$属于[0, 1]之间。但是，这样的得分并不能够很好地预测概率。

我们可以举出几个上述描述的分类器，比如朴素贝叶斯（Naive Bayes）和支持向量机（SVM）。让我们回忆一下，当我们使用朴素贝叶斯分类器时，我们将某测试样本属于各种类别的概率全部计算出来，选择概率最大的类别作为该测试样本的预测标签，对应的概率可以视为一个得分；当我们使用支持向量机时，我们将某测试样本的属性代入求出的分隔超平面上，预测出该测试样本对应的标签。或可将该测试样本与分隔超平面的距离作为得分的函数，即距离越大，分数越高，属于对应类别的概率越大。然而，这两个分类器给出的所谓“得分”并不能很好地预测属于对应类别的概率。

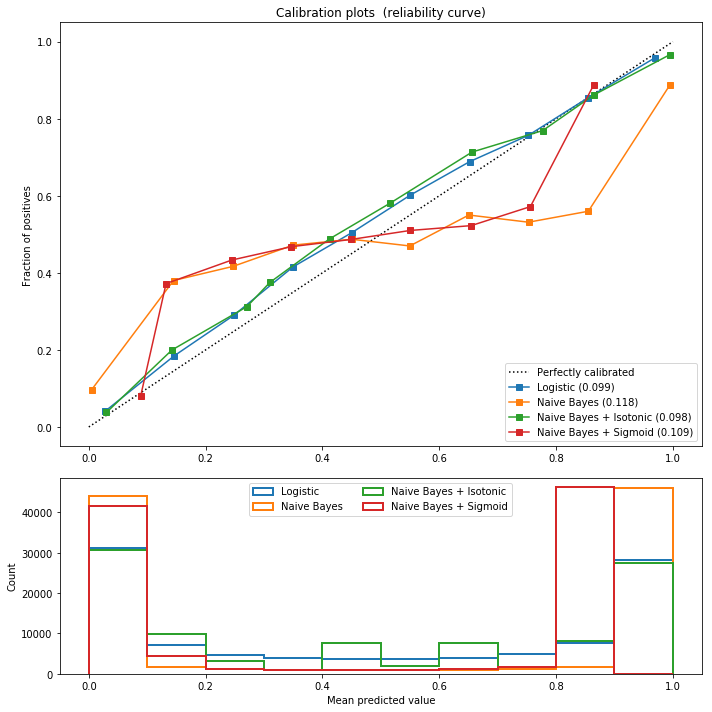
如果一个得分函数$S(x)$是预测概率的较好估计，它应该满足以下条件。对于一系列测试样本，我们的平均得分$S(x)$应该与测试样本的真实属于某类别的概率比较接近。我们可以用可靠性图（Reliability Plot）来直观地帮助我们判断预测的概率和真实概率之间的差距。一般而言，在可靠性图中，每个点的横坐标为得分函数$S(x)$，纵坐标为经验的测试数据的概率，图中的直线为y=x，可用作参考。

在图中，我们可以发现，虽然可靠性图中的点在直线y=x周围起起伏伏，然而，倒也满足这样的条件，如果$S(x_i)<=S(x_j)$，那么$r(x_i) <= r(x_j)$。由于有此优良性质，我们考虑将得分函数$S(x)$映射到经验的概率估计值。这一过程，我们称为概率校准。也即找到这样一个映射函数，满足$P(c|x) = f(S(x))$。

2. 映射函数

在实际应用中，一般有两种形式的映射函数可供参考。一种为保序回归，另一种为Platt Scaling。

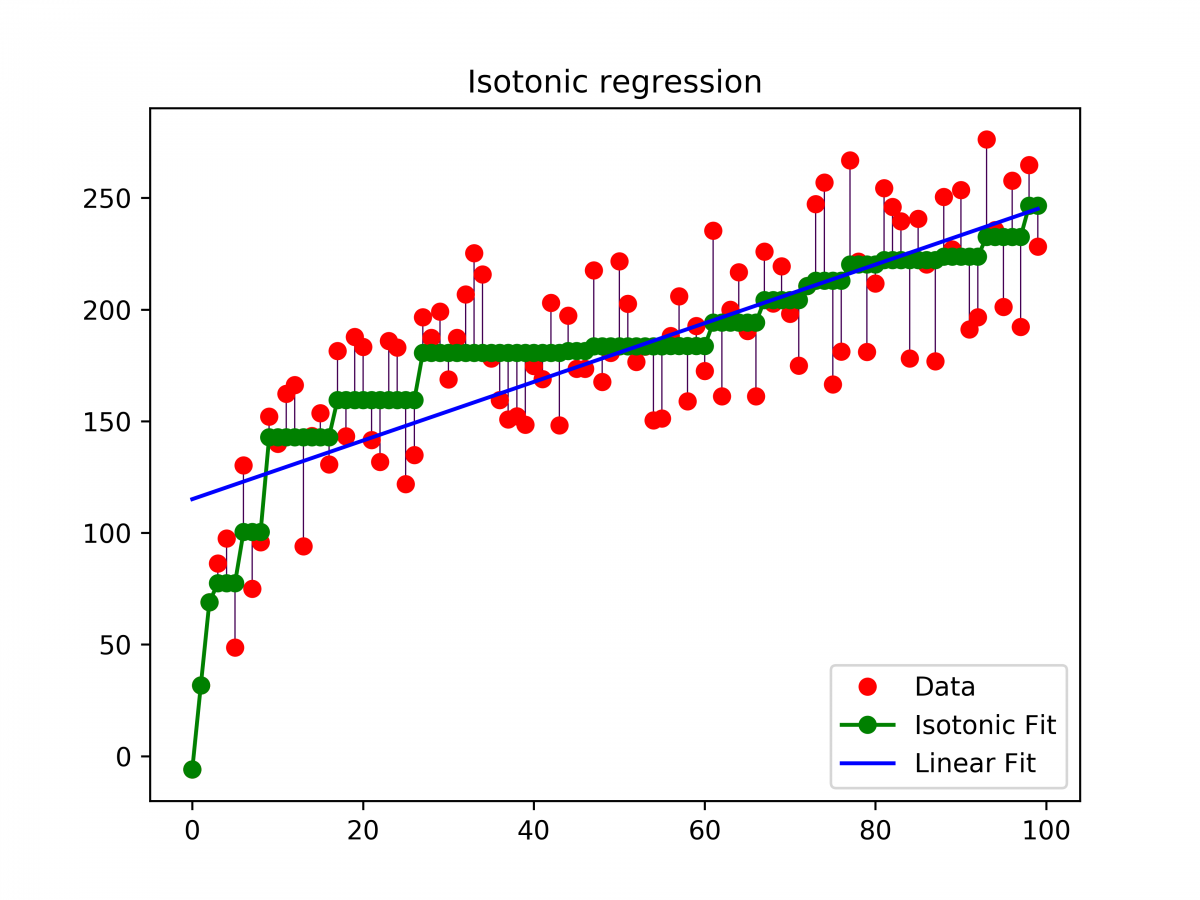
(1) 保序回归

保序回归的应用背景之一为临床试验研究药物在不同剂量水平下的毒性，以得到最大耐受剂量（MTD）。固定K个递增的剂量水平，我们的假设为随着剂量的上升，药物的毒性应该是非递减的。然而，在实际临床实验中，由于各个剂量水平下，实验个体对于毒性反应的比例可能受各类因素影响，不一定呈现递增的毒性反应。因而，我们需要采用保序回归方法。

给定$x_1<=x_2<=…<=x_n$, $t = 1, 2, …, n$

sigma(yit - y_it)^2

我们关注$x_1, …, x_n$的排序，而非它们具体的取值

该回归问题的目标为寻找一个非递减的函数来最好地预测回归的响应变量。

Pool-Adjacent-Violators Algorithm (PAVA)

PAVA算法是解决单调性回归问题的一种较为简单的非参数方法。假设，我们按照自变量的顺序将数据排序，得到以下序列组$(x_i, y_i), i = 1, …, n.$

step=1, $z_1 = y_1$
step=2, if $y_2<z_1$, then $s_1 = y_1 + y_2$, $z_1 = z_2 = s_1/2$; else $z_2 = y_2$
…
step = k, if $yk<z{k-1}$, then $s_m = yj+y{j+1} + … +y_k$, $zj=z{j+1}=…=z_k=s_m/{k-j+1}$; else $z_k = y_k$

举例：

x = [1, 2, 3, 5]; y = [2, 4, 6, 7]; z = [2, 4, 6, 7]
x = [1, 2, 3, 5]; y = [6, 4, 6, 7]; z = [5, 5, 6, 7]
x = [1, 2, 3, 5]; y = [6, 4, 2, 7]; z = [4, 4, 4, 7]

music

(2) Platt Scaling

Platt scaling最早的引入是一种为了校正SVM概率的方法，可以使得SVM的输出空间从[-∞, +∞]映射到[0, 1]。具体的目标为，找到一个sigmoid函数的参数使得训练集上的似然函数最大。函数如下所示：

$$P(c|s) = \frac{1}{1+{\rm e}^{As+B}}$$

其中，$P(c|s)$ 为某个测试样本属于类别c的概率，$s$为该测试样本在分类器的得分，$A$和$B$是函数的参数。

另外，Friedman, Hastie, 和Tibshirani提出Logistic correction来校正Boosted模型。

3. 评判标准

Brier Score
在N次预测中，Brier score是均方误差，衡量的是
(1)对于测试样本i属于类别c的预测概率
(2)实际结果
两者之间的均方误差。因而，对于一系列的预测而言，Brier score越低，说明预测的概率越准确。Brier score的适用范围为二元属性类别的预测情况，不适用于定序（或超过两种类别）的预测。

4. Python Sklearn中的概率校准

关键函数CalibratedClassifierCV(base_estimator=None, method=’sigmoid’, cv=3)
参数：

base_estimator
method：’isotonic’ 或者 ‘sigmoid’。适用情况：isotonic适用于校准样本小于1000的情况，
cv：
- None
- integer
- cross-validation generator
- iterable
- “prefit”

https://stackoverflow.com/questions/30285551/why-does-calibratedclassifiercv-underperform-a-direct-classifer

具体参考Probability Calibration

# Author: Alexandre Gramfort <alexandre.gramfort@telecom-paristech.fr>
#         Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD Style.
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (brier_score_loss, precision_score, recall_score,
                             f1_score)
from sklearn.calibration import CalibratedClassifierCV, calibration_curve
from sklearn.model_selection import train_test_split

导入所用的package，包括sklearn里面的Naive Bayes，SVM和Logistic回归。同时，引入所需要的概率校准的方法CalibratedClassifierCV。

# Create dataset of classification task with many redundant and few
# informative features
X, y = datasets.make_classification(n_samples=100000, n_features=20,
                                    n_informative=2, n_redundant=10,
                                    random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.99, random_state=42)

创建一个用作分类的数据集，该数据集包含10000个样本，20个特征，其中，有信息的特征为2个，重复性的特征有10个。并且，针对该数据集，我们将1%的数据作为训练集，99%的数据作为测试集。

"""Plot calibration curve for est w/o and with calibration. """
# Calibrated with isotonic calibration
isotonic = CalibratedClassifierCV(GaussianNB(), cv=2, method='isotonic')
# Calibrated with sigmoid calibration
sigmoid = CalibratedClassifierCV(GaussianNB(), cv=2, method='sigmoid')
# Logistic regression with no calibration as baseline
lr = LogisticRegression(C=1., solver='lbfgs')

对Gaussian假设的Naive Bayes建立两种概率校准模型，一种为istonic，即保序回归，另一种为sigmoid函数。
同时，创建一个供参考的基准模型，即不做任何概率校准的logistic回归模型。

fig = plt.figure(1, figsize=(10, 10))
ax1 = plt.subplot2grid((3, 1), (0, 0), rowspan=2)
ax2 = plt.subplot2grid((3, 1), (2, 0))
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
for clf, name in [(lr, 'Logistic'),
                  (GaussianNB(), "Naive Bayes"),
                  (isotonic, "Naive Bayes" + ' + Isotonic'),
                  (sigmoid, "Naive Bayes" + ' + Sigmoid')]:
    clf.fit(X_train, y_train)
    y_pred = clf.predict(X_test)
    if hasattr(clf, "predict_proba"):
        prob_pos = clf.predict_proba(X_test)[:, 1]
    else:  # use decision function
        prob_pos = clf.decision_function(X_test)
        prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
    clf_score = brier_score_loss(y_test, prob_pos, pos_label=y.max())
    fraction_of_positives, mean_predicted_value = calibration_curve(y_test, prob_pos, n_bins=10)
    ax1.plot(mean_predicted_value, fraction_of_positives, "s-", label="%s (%1.3f)" % (name, clf_score))
    ax2.hist(prob_pos, range=(0, 1), bins=10, label=name, histtype="step", lw=2)
ax1.set_ylabel("Fraction of positives")
ax1.set_ylim([-0.05, 1.05])
ax1.legend(loc="lower right")
ax1.set_title('Calibration plots  (reliability curve)')
ax2.set_xlabel("Mean predicted value")
ax2.set_ylabel("Count")
ax2.legend(loc="upper center", ncol=2)

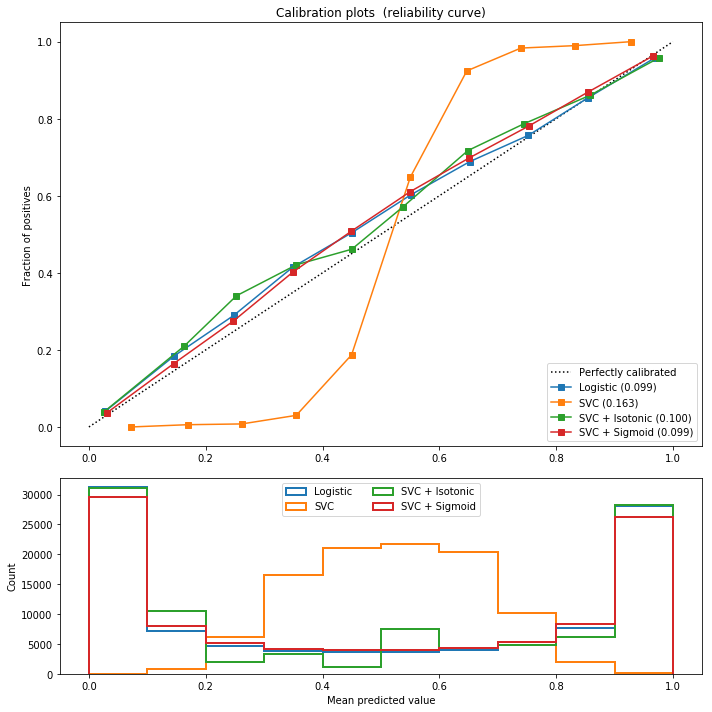
画图过程，对比4张Reliability图，朴素贝叶斯、保序回归概率校准的朴素贝叶斯、sigmoid概率校准的朴素贝叶斯，以及logistic回归。类似的，我们可以对支持向量机（SVM）做类似的概率校准，得到相应的Reliability图。
music
music